Построение параллельных прямых

1. Изображение параллельных прямых с применением угольника и линейки
2. Изображение параллельных прямых с использованием циркуля и линейки
3. Изображение параллельной прямой, отдаленной на определенное расстояние от имеющейся
4. Прочие способы изображения параллельных прямых

Для изображения в пространстве прямых, что параллельны друг другу, с использованием разнообразных инструментов опираются на свойства их параллельности.

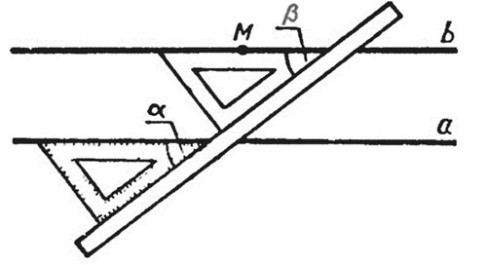
Изображение параллельных прямых с применением угольника и линейки

Используем принцип изображения параллельной прямой, что пересекает заданную точку, с использованием чертежного угольника и линейки. Рассмотрим порядок действий при этом способе построения. Допустим, изображены прямая a и точка \(M\), не лежащая на ней:

1. Диагональ угольника совмещаем с прямой a, а вдоль его большого катета фиксируем линейку;
2. Перемещаем угольник вдоль линейки до того момента, пока диагональ не сравняется с точкой \(M\);
3. Чертим через точку \(M\) вдоль диагонали угольника прямую \(b\). Она и будет параллельна существующей прямой \(a\).
4. Параллельность этих прямых подтверждается также равностью углов \(∝\) и \(β\).
    

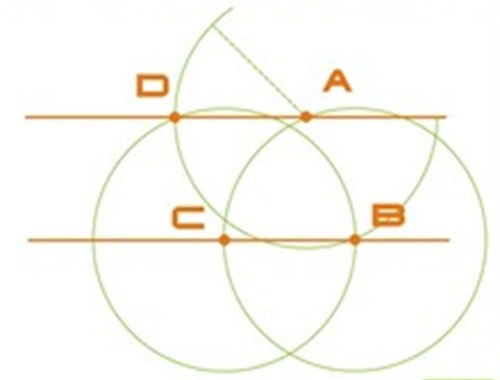
Изображение параллельных прямых с использованием циркуля и линейки

Также широко применяется способ изображения параллельных прямых с применением линейки и циркуля.

Допустим есть прямая и точка \(A\), не лежащая на ней. Необходимо изобразить прямую, параллельную существующей прямой и пересекающую заданную точку \(A\).

Часто требуется просто изобразить параллельные прямые без начальных условий. В подобном варианте просто нужно самостоятельно изобразить прямую и поставить точку, не лежащую на этой прямой.

Итак, порядок изображения параллельной прямой:

1. Выбираем случайную точку на существующей прямой, дадим ей название, например \(B\). Выбираем совершенно любую точку, это не повлияет на результат;
2. С помощью циркуля чертим круг с центром в точке \(B\) и радиусом \(AB\);
3. Ккруг проходит через прямую в точке, которую назовем \(C\);
4. Начертим еще один круг радиусом \(AB\), но уже с центром в точке \(C\). Стоит заметить, что этот круг должен в любом случае пересечь точку \(B\), если все выполнено верно;
5. Этим же радиусом чертим круг с центром в точке \(A\);
6. Этот круг пересечет предыдущий в точке, которую назовем \(D\). Также стоит учесть, что и этот круг при верном построении пересечет точку \(B\);
7. На данном этапе через точки \(A\) и \(D\) проводим с использованием линейки прямую, она будет параллельна существующей прямой.

В итоге мы имеем две прямые \(BC\) и \(AD\), параллельные между собой.

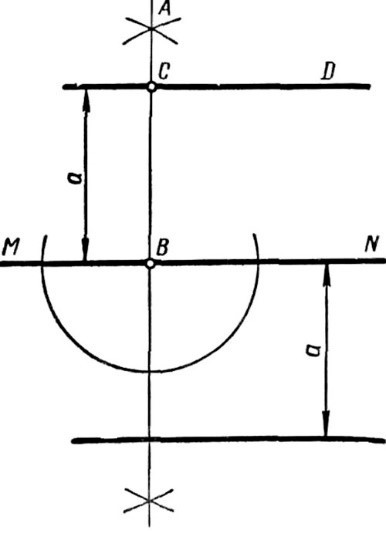
Изображение параллельной прямой, отдаленной на определенное расстояние от имеющейся

Для изображения параллельной прямой, относительно имеющейся, на определенном конкретном расстоянии можно использовать угольник и линейку. \(К\) примеру, изображена прямая \(MN\) и задано некое расстояние \(a\):

1. Отмечаем на существующей прямой \(MN\) случайную точку, например назовем ее \(B\);
2. Теперь необходимо изобразить прямую через точку \(B\), перпендикулярную изображенной прямой. Назовем ее  \(AB\);
3. Откладываем на построенной прямой отрезок \(BC\), который равен \(a\);
4. С использованием линейки и угольника, как описано выше, проведем через точку \(C\) прямую \(CD\), она будет параллельной к прямой \(MN\).

Возможно также на прямой \(AB\) отмерить расстояние \(a\) от точки \(B\) в противоположную сторону, проделать все вышеописанное и начертить еще одну прямую параллельно существующей прямой \(MN\).

Прочие способы изображения параллельных прямых

В чертежной сфере часто применяют способ изображения с использованием рейсшины. Столяры при изготовлении изделий часто используют так называемый инструмент – малку, состоящую из двух планок на шарнирах. Этим инструментом наносят разметку с использованием принципов параллельных прямых.