Лабораторная работа 1-25: Определение удельной теплоты кристаллизации и изменения энтропии при охлаждении олова
Цель работы: определение изменения энтропии при фазовом переходе первого рода на примере кристаллизации олова из расплава при его охлаждении; определение теплоты кристаллизации олова из закона сохранения энергии.
Приборы и принадлежности: ампула с оловом, хромель- копелевая термопара, плавильная печь.
Теория и метод эксперимента
Теоретические сведения
В термодинамике фазой называется макроскопическая физическая однородная часть вещества, отделённая от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путём.
Допустим, например, что в закрытом сосуде заключена некоторая масса воды, над которой находится смесь воздуха с водяными парами. Эта система является двухфазной. Если бы воздуха не было, то в системе также было бы две фазы: жидкая (вода) и газообразная (водяные пары). При появлении в воде кусочков льда система превратится в трёхфазную и будет состоять из твёрдой фазы (лёд), жидкой (вода) и газообразной (смесь воздуха с водяными парами). Если добавить к воде некоторое количество спирта, то число фаз не изменится, так как вода смешивается со спиртом, образуя физически однородную жидкость.
При подсчёте числа фаз не имеет значения, является та или иная фаза единым телом или состоит из нескольких частей, отделённых одна от другой.
Важнейшим вопросом является выяснение условий, при которых система, состоящая из двух или нескольких фаз, находится в равновесии. Последнее включает в себя механическое и тепловое равновесие. Для теплового равновесия необходимо, чтобы все фазы системы имели одну и ту же температуру. Необходимым условием механического равновесия является равенство давлений по разные стороны границы раздела сопри- касающихся фаз.
Равенство давлений и температур ещё не означает, что система находится в равновесии, так как соприкасающиеся фазы могут превращаться друг в друга. Такие превращения называются фазовыми превращениями. При фазовых превращениях одни фазы растут, другие уменьшаются и даже могут совсем исчезнуть. Состояние равновесия характеризуется тем, что массы всех фаз системы остаются неизменными. Следовательно, должно быть выполнено ещё одно необходимое условие равновесия – равновесие по отношению к взаимным превращениям фаз.
Вообще фазовое равновесие между любыми двумя фазами не является статическим состоянием, в котором полностью прекращаются фазовые превращения, а характеризуется равенством средних скоростей двух взаимно противоположных процессов: превращения первой фазы во вторую и обратного превращения второй фазы в первую. При равновесии эти противоположные процессы взаимно компенсируют друг друга, как того требует принцип детального равновесия. Благодаря этому количество вещества в каждой фазе в среднем остаётся неизменным.
Примерами фазовых превращений могут служить изменения агрегатного состояния вещества. Под агрегатными состояниями понимают твёрдое, жидкое и газообразное состояния вещества. Переход вещества из одной фазы в другую обычно сопровождается поглощением или вы- делением некоторого количества теплоты, которая называется теплотой фазового превращения. Например, при таянии льда поглощается теплота плавления, при замерзании воды выделяется такое же количество теплоты. Переходы, сопровождающиеся поглощением или выделением теплоты, называются фазовыми превращениями первого рода.
Твёрдое и жидкое состояния называются конденсированными. Парообразованием называют переход вещества из конденсированного состояния в газообразное. Обратный переход называется конденсацией. Парообразование, происходящее только на поверхности жидкости, называется испарением. Парообразование по всему объему жидкости называется кипением. Оно происходит при определенной температуре, зависящей от давления. Переход из твёрдого состояния непосредственно в газообразное называется сублимацией или возгонкой. Переход из твёрдого состояния в жидкое называется плавлением, а обратный переход из жидкого состояния в твёрдое – затвердеванием или кристаллизацией.
Твёрдое состояние вещества может реализоваться в различных кристаллических модификациях. Это явление называется полиморфизмом. Например, твёрдый углерод может существовать в виде графита или алмаза, которые отличаются друг от друга кристаллической структурой. При изменении температуры и давления вещества могут переходить из одной кристаллической модификации в другую. Такие превращения также относятся к числу фазовых превращений. Они не связаны с поглощением или выделением теплоты и называются фазовыми превращениями второго рода. При фазовых превращениях второго рода плотность вещества не изменяется, в то же время скачкообразно изменяются удельная теплоёмкость и некоторые другие величины. Примером превращения второго рода может служить переход железа из ферромагнитного со- стояния в парамагнитное, который происходит при температуре, называемой точкой Кюри.
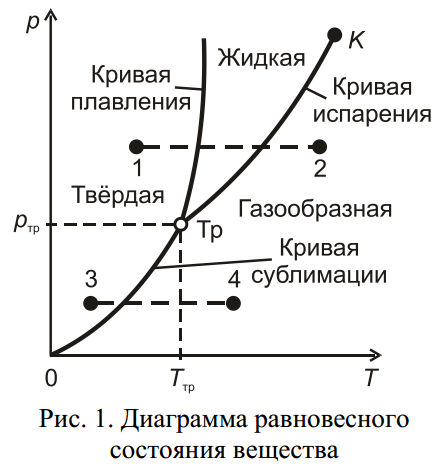
Совокупность состояний равновесия нескольких фаз изображается на диаграмме состояния вещества ( p, T ) кривыми p = f (T ) (см. рис. 1).
Эти кривые определяют такие состояния, в которых вещество при неизменных внешних условиях пребывает сколь угодно долго. Строятся диаграммы равновесных состояний на основе экспериментальных данных.
Кривые плавления, испарения и сублимации разбивают координатную плоскость p — T на три области. Слева от кривых сублимации и плавления лежит область твёрдой фазы, между кривыми плавления и испарения заключена область жидких состояний, и, наконец, справа от кривых испарения и сублимации простирается область газообразных со- стояний. Всякая точка в одной из этих областей изображает соответствующее однофазное состояние вещества. Любая точка, лежащая на одной из разграничивающих области кривых, определяет условия равновесия двух соответствующих фаз вещества. Три фазы одного и того же вещества (твёрдая, жидкая и газообразная, или жидкая и две твёрдые, или, наконец, три твёрдые) могут находиться в равновесии только при единственных значениях температуры и давления, которым на диаграмме ( p, T ) соответствует точка, называемая тройной. В тройной точке сходятся три кривые равновесия фаз, взятых попарно (рис. 1).
Диаграмма состояния позволяет определить, какие превращения будет претерпевать вещество при различных процессах. Например, если взять вещество в состоянии, изображаемом точкой 1 на рис. 1, и подвергнуть его изобарическому нагреванию, то вещество будет проходить изображённую штриховой прямой 1–2 последовательность состояний: кристаллы – жидкость – газ. Если же взять вещество в состоянии, изображаемом
точкой 3, и также подвергнуть изо- барическому нагреванию, то последовательность состояний 3–4 будет иной: кристаллы превращаются непосредственно в газ, минуя жидкую фазу.
В данной работе изучается одно из фазовых превращений вещества – затвердевание, или кристаллизация. Процесс кристаллизации связан с выделением количества теплоты, равного теплоте плавления. Для химически чистых веществ процесс кристаллизации протекает при постоянной температуре, равной температуре плавления. В процессе кристаллизации упорядочивается движение частиц жидкости, постепенно прекращается перемещение молекул, возникают связанные тепловые колебания относительно узлов кристаллической решётки. Для начала кристаллизации необходимо, чтобы в жидкости имелись центры кристаллизации – неоднородности, вокруг которых начинается процесс образования твердой фазы. Если в жидкости отсутствуют центры кристаллизации, то она может быть охлаждена до температуры, более низкой, чем температура кристаллизации. В обычных условиях этого, как правило, не происходит.
Количество теплоты, которое необходимо отвести от единицы массы жидкости при температуре кристаллизации для перехода жидкости в твердое состояние, называется удельной теплотой кристаллизации.
Из первого начала термодинамики следует:
$$\lambda_{кр}=U_{тв}-U_{ж}+P(V_{тв}+V_ж)$$
где Uтв и Uж внутренняя энергия единицы массы в твёрдом и жидком
состояниях; Vтв и Vж удельный объём твёрдой и жидкой фазы соответственно; P – давление в процессе кристаллизации. Поскольку при переходе из жидкого в твердое состояние объем олова практически не меняется, имеем P(Vтв —Vж )Uтв —Uж . В этом случае
$$\lambda_{кр}\approx U_{тв}-U_{ж}$$
Формула 1
Простейшей моделью охлаждения тела является охлаждение в среде с постоянной температурой Tср (в термостате). Если процесс охлаждения происходит достаточно медленно, температуру произвольной точки тела в каждый момент времени можно считать одинаковой. Такой процесс охлаждения состоит из непрерывно следующих друг за другом равновесных состояний и, следовательно, является квазистатическим обратимым процессом.
Применим закон сохранения энергии к квазистатическому процессу охлаждения твердого олова после кристаллизации:
$$(c_0M_0+c_aM_a)dT+\alpha \sigma(T-T_{ср})d\tau=0$$
Формула 2
(coMo + ca Ma )dT < 0 — количество теплоты, отданное телом среде при его охлаждении за время dt;
as(T — Tср )dt > 0 — количество теплоты, полученное окружающей средой через поверхность ампулы площадью s за время dt;
c0 и ca — удельные теплоёмкости олова и материала ампулы;
M0 и Ma массы олова и ампулы;
T – температура твёрдого олова;
Tср — температура окружающей среды;
a – коэффициент теплоотдачи с поверхности ампулы в окружающую среду.
Применяя закон сохранения энергии к процессу кристаллизации олова, можно получить уравнение
$$\lambda_{кр}M_0+\alpha \sigma(T_{кр}-T_{ср})\triangle \tau_{кр}=0$$
Формула 9
где λкрM0= Qкр количество теплоты, отданное оловом при его кристаллизации за время кристаллизации Dtкр . Так как тепло отдано окружающей среде, то Qкр < 0 .
Второй член суммы ασ(Tкр−Tср)△τкр > 0 – количество теплоты, полученное окружающей средой через поверхность ампулы за время кристаллизации.
Из соотношений (2) и (3) следует, что
$$\lambda_{кр}=(c_0M_0+c_aM_a)\frac{\triangle \tau_{кр}}{M_0}\frac{ T_{кр}-T_{ср}}{T-T_{ср}}\frac{dT}{d \tau}$$
Формула 4
Процесс кристаллизации можно описать функцией состояния термодинамической системы – энтропией. Понятие энтропии впервые было введено в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации – мера неопределённости какого-либо опыта, который может иметь разные исходы.
Пусть dQ – элементарное количество теплоты, полученное или отданное системе при малом изменении её состояния, а T – термодинамическая температура нагревателя или холодильника, изменяющего состояние этой системы. Тогда отношение dQ T в обратимом процессе является полным дифференциалом функции состояния системы, то есть энтропии S . Таким образом, в обратимом процессе температура T является интегрирующим делителем, который обращает элементарную теплоту dQ в полный дифференциал dS :
dS = dQ/T (обратимый процесс).
Если термодинамической системе сообщается количество теплоты dQ в ходе необратимого процесса, то энтропия получает, кроме приращения dQ/T , знак которого совпадает со знаком dQ , положительное приращение, обусловленное необратимостью процесса. В итоге
dS > dQ/T (необратимый процесс).
Отсюда следует, что при протекании необратимого процесса в системе, отдающей теплоту внешней среде (dQ<0), энтропия может не только возрастать, но и убывать. Это будет иметь место в том случае, когда |dQ/T| больше той доли приращения энтропии, которая обусловлена необратимостью процесса.
Из определения энтропии как величины, характеризующей вероятность состояния термодинамической системы, вытекают следующие её свойства:
а) в ходе необратимого процесса энтропия термодинамической системы возрастает;
б) энтропия термодинамической системы, находящейся в равновесном состоянии, максимальна.
Утверждение о том, что энтропия термодинамической системы может только возрастать либо по достижении максимального значения оставаться постоянной, носит название закона возрастания энтропии или второго начала термодинамики.
С учётом вышесказанного разность энтропии в двух состояниях при обратимом процессе равна
$$S_2-S_1=\int_1^2 \frac{\delta Q}{T}$$
Формула 5
В процессе кристаллизации олово отдаёт тепло окружающей среде при T = const . При этом количество теплоты, отданное окружающей среде,
$$Q_{кр}=\lambda_{кр}M_0$$
Формула 6
Из (5) и (6) с учётом (1) следует, что
$$S_2-S_1=\frac{\lambda_{кр}M_0}{T_{кр}}$$
или
$$S_2-S_1=\frac{(U_{тв}-U_ж)M_0}{T_{кр}}$$
В процессе кристаллизации происходит упорядочивание структуры вещества, внутренняя энергия вещества уменьшается, что и приводит к убыванию энтропии системы.
Описание экспериментальной установки
Вид экспериментальной установки изображён на рис. 2. На перед- ней панели расположены: цифровой индикатор термометра 2, тумблер включения питания «сеть» 7, тумблер включения электропитания печи «нагрев» 6, тумблер включения электропитания термометра 1.
Ампула с оловом 4 опускается с помощью устройства перемещения в электрическую печь 8, питающуюся переменным током, и нагревается в ней. По окончании плавления всей массы олова ампула должна подниматься из печи и подъёмное устройство стопорится винтом 5.
Электрическая печь 8 находится внутри корпуса экспериментальной установки 3. Внутри ампулы находится металлическая трубка-чехол 10, в которую помещён термодатчик 9. В качестве термодатчика в дан- ной установке используется дифференциальная хромель-копелевая термопара, горячий спай которой находится в ампуле, а холодный спай — на воздухе. Датчик температуры соединён с цифровым индикатором температуры 2.

Методика эксперимента
Для определения удельной теплоты кристаллизации олова и изменения энтропии при фазовом переходе первого рода необходимо измерить температуру кристаллизации Tкр , время кристаллизации олова Dtкр, а также вычислить производную dT dt функции T =f (t) во время охлаждения твёрдого олова после полной кристаллизации. Эти величины можно найти, измерив температуру олова в процессе охлаждения от полного расплава до температуры остывшего олова в конце опыта.
В принятой модели процесс охлаждения твёрдого олова от точки полной кристаллизации описывается уравнением (4). Решение этого уравнения имеет вид:
$$\theta=\theta_{кр}e^{-m(\tau-\tau_{кр})}$$
Формула 8
τ – момент времени полной кристаллизации. Коэффициент m называют темпом охлаждения. Он характеризует относительную скорость изменения температуры тела. Темп охлаждения можно определить из линейной зависимости, полученной логарифмированием функции (8):
$$ln \theta=ln \theta_{кр}-m(\tau-\tau_{кр})$$
Формула 9
По тангенсу угла наклона прямой, определяемой выражением (9), рассчитывается относительная скорость изменения температуры олова (темп охлаждения):
m=\frac{ln \theta_{кр}-ln \theta}{(\tau-\tau_{кр})}$$m=\frac{ln \theta_{кр}-ln \theta}{(\tau-\tau_{кр})}$$
Формула 10
Учитывая (10) и (4), находим удельную теплоту кристаллизации олова
$$\lambda_{кр}=-(с_0M_0+c_aM_a)\frac{\triangle \tau_{кр}}{M_0}m \theta_{кр}$$
Формула 11
и изменение энтропии при фазовом переходе первого рода
$$\triangle S=S_2-S_1=-(c_0M_0+c_aM_a)\frac{\triangle \tau_{кр}}{T_{кр}}m \theta_{кр}$$
Формула 12
Реальный процесс охлаждения сопровождается явлениями, вносящими погрешность в определение удельной теплоты кристаллизации λкр.
Главными источниками погрешности являются:
- отклонение процесса охлаждения от квазистатического;
- изменения температуры окружающей среды.
Эти процессы приводят к методической погрешности определения λкр, не превышающей ±10 %.
Порядок выполнения работы
- Убедившись, что все тумблеры находятся в нижнем положении, включите в сеть шнур питания установки. Переведите переключатель «сеть» на лицевой панели в верхнее положение.
- Ослабьте стопорный винт 5 подъёмного устройства и опустите ампулу с оловом 4 в плавильную электрическую печь 8. Включите тумблерами «нагрев» и «термометр» электропитание плавильной печи и индикатора термометра 2. При этом температура внутри ампулы, отображаемая индикатором в °С, должна постепенно увеличиваться со временем.
В течение 10-15 мин олово, находящееся в стальной ампуле, должно расплавиться. Процесс плавления олова должен происходить при постоянной температуре плавления Tпл . При этом показания индикатора температурного датчика практически не изменяются. Окончание процесса плавления можно определить как момент времени, после которого температура начинает резко возрастать. Для данной установки Tпл »163 ¸168 °C.
3. При достижении температуры олова T =190 °C отключите электропечь тумблером «нагрев», ослабьте стопорный винт 5, подними- те ампулу с оловом, вытащив её из печи, и зафиксируйте это положение ампулы стопорным винтом.
4. Используя секундомер, через каждые 10-20 с снимайте показания цифрового индикатора термометра. Измерения продолжайте до тех пор, пока не будут пройдены три области процесса охлаждения (рис. 3): I – область расплава, II – область кристаллизации и III – область охлаждения твёрдого олова. Время опыта должно составлять не менее 14-16 мин. Данные занесите в табл. 1.
Таблица 1
Данные эксперимента

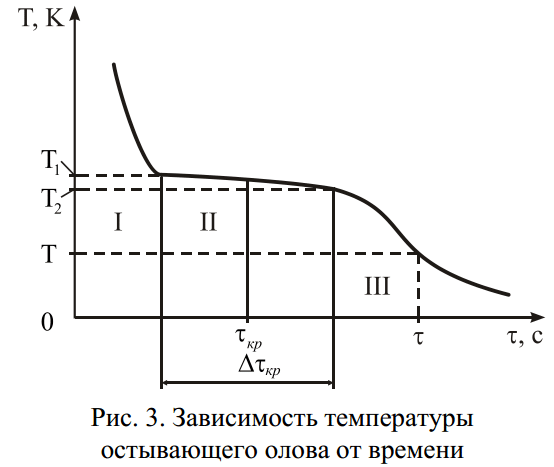
Постройте график зависимости температуры олова от времени T = f (t) . Определите интервал времени кристаллизации олова Dtкр (ширина плато на графике) и температуру кристаллизации олова как среднюю температуру области кристаллизации
Tкр = (T1 + T2 ) 2, а также момент времени полной кристаллизации tкр по графику T = f (t) (см. рис. 3).
Постройте график зависимости логарифма температуры остывающего олова от времени ln q = f (t — tкр ) . Используя соотношение
(10), по тангенсу угла наклона кривой определите относительную скорость изменения температуры тела (темп охлаждения) m .
Рассчитайте удельную теплоту кристаллизации олова λкр и изменение энтропии при фазовом переходе первого рода по формулам (11) и (12) соответственно. Данные экспериментальной установки приведены в табл. 2.
Таблица 2
Данные лабораторной установки

Учитывая изменение температуры во время кристаллизации олова (область II на рис. 3), определите абсолютную погрешность температуры кристаллизации Tкр по формуле:
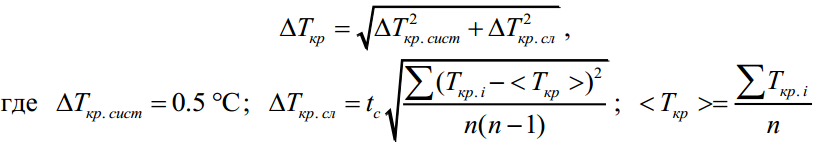
среднее значение температуры кристаллизации олова;
Tкр. i
- i-е значение температуры олова на участке кристаллизации II (см. рис. 3); n –общее число значений
Tкр. i
в пределах области кристаллизации; tc
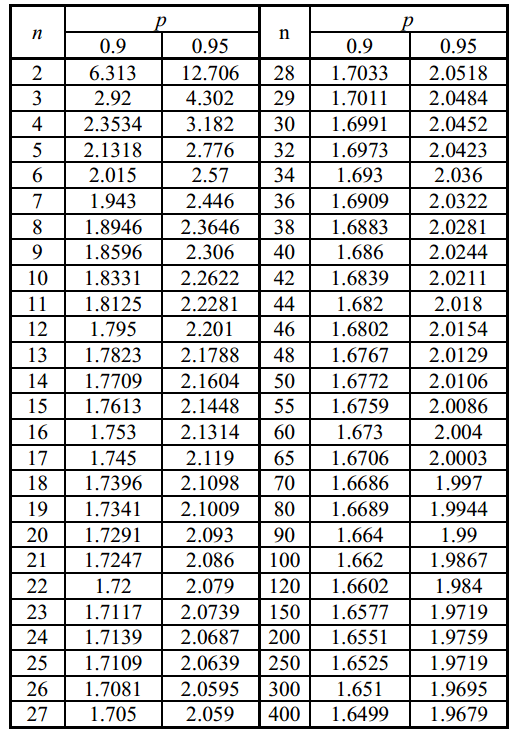
- коэффициент Стьюдента, значение которого выбирается из таблицы приложения.

Вычислите абсолютную и относительную погрешности изменения эн- тропии при фазовом переходе первого рода по следующим выражениям:

Вопросы и задания для самоконтроля
-
Что называется фазой термодинамической системы? Фазовые превращения вещества первого и второго рода.
.
-
Что представляет собой диаграмма равновесного состояния вещества? Чем определяется тройная точка на этой диаграмме?
.
-
Что называется процессом кристаллизации вещества? Какие условия нужны для возникновения этого процесса?
.
-
Как изменяется внутренняя энергия вещества при его переходе из жидкого состояния в твёрдое?
.
-
Что называется удельной теплотой кристаллизации? Вывести выражение (11), определяющее удельную теплоту кристаллизации олова при остывании.
.
-
Сформулируйте второе начало термодинамики. Объясните, что называется энтропией. Каковы свойства этой функции состояния термодинамической системы?
.
-
Объясните методику эксперимента.
.
Библиографический список
- Савельев И.В. Курс физики. T. 1. Механика. Молекулярная фи- зика. М.: Наука, 1989. C. 315-325.
- Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие для ву- зов. 8-е изд., стереотип. М.: Академия, 2009. С. 154-166.
- Сивухин Д.В. Общий курс физики. Т. 2. Термодинамика и моле- кулярная физика. М.: Физматлит, 2003. С. 457-496.
Приложение
Значения коэффициента Стьюдента для величин доверительной вероятности p = 0.9; 0.95 и различного числа измерений n
УДК 536.421
Определение удельной теплоты кристаллизации и изменения энтропии при охлаждении олова: методические указания к лабораторной работе / Рязанский государственный радиотехнический университет; сост.: А.В. Брыков, А.Е. Малютин. Рязань: РГРТУ, 2016. 12 с.
Рассматривается теория фазовых превращений первого и второго рода, представлен метод определения удельной теплоты кристаллизации вещества и изменения энтропии при фазовом переходе первого рода. Приводятся порядок выполнения работы, методические указания по расчету погрешностей, контрольные вопросы и список рекомендуемой литературы.
Предназначены для студентов всех специальностей, изучающих дисциплину «Физика».
Табл. 3. Ил. 3. Библиогр.: 3 назв.
Кристаллизация, количество теплоты, удельная теплота плавления и кристаллизации, температура, энтропия, темп охлаждения твёрдого тела, фазовый переход
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Определение удельной теплоты кристаллизации и изменения энтропии при охлаждении олова
Составители: Брыков Александр Валериевич Малютин Александр Евгеньевич
Редактор Р.К. Мангутова Корректор С.В. Макушина
Подписано в печать 10.03.16. Формат бумаги 60 x 84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,75.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТУ.
