МУ 4666: Определение моментов инерции тел с помощью маятника Максвелла
Лабораторная работа 1-17: Определение моментов инерции тел с помощью маятника Максвелла
Цель работы: экспериментальное определение моментов инерции сменных колец с помощью маятника Максвелла.
Приборы и принадлежности: установка с маятником Максвелла, блок электронный ФМ-1/1, набор сменных колец.
Элементы теории и метод эксперимента
Маятник Максвелла наглядно демонстрирует закон сохранения механической энергии и, кроме того, с его помощью можно определить момент инерции тела.
Механическая энергия системы – сумма кинетической и потенциальной энергий. Когда действуют только консервативные силы, то механическая энергия не изменяется со временем.
Момент инерции является мерой инертности тела при вращательном движении. Для системы материальных точек момент инерции определяется по формуле
$$J=\sum_{i=1}^nm_ir_i^2$$
где mi – масса i-й материальной точки, ri – расстояние от материальной точки до оси вращения.
Для вычисления момента инерции протяженного тела плотностью ρ его разбивают на элементарные объемы dV массой dm и момент инерции тела определяют путем интегрирования по всему объему:
$$J=\int_mr^2dm=\rho \int_V r^2dV$$
Изображение маятника Максвелла показано на рис. 1. Маятник представляет собой диск 1, закрепленный на стержне 2, подвешенном на бифилярном подвесе 3.
На диске могут крепиться сменные кольца 4. На вертикальной стойке основания крепятся два кронштейна. Верхний кронштейн 5 снабжен электромагнитом 6 и устройством регулировки бифилярного подвеса 7.
С помощью электромагнитов маятник со сменными кольцами фиксируется в верхнем исходном положении.
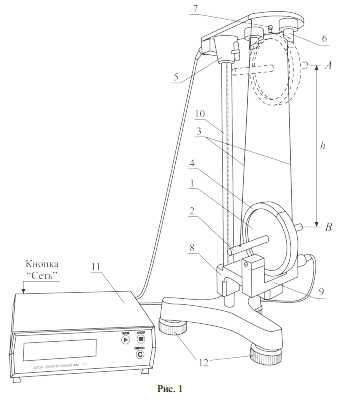
На нижнем кронштейне 8 закреплен фотоэлектрический датчик 9. Кронштейн обеспечивает возможность перемещения датчика вдоль вертикальной стойки 10.
На стойке нанесена миллиметровая шкала, по ко- торой определяется ход h маятника. Фотодатчик выдает электрические сигналы на миллисекундомер 11.
Основание расположено на трёх регулировочных опорах 12, позволяющих устанавливать стойку 10 в вертикальное положение.
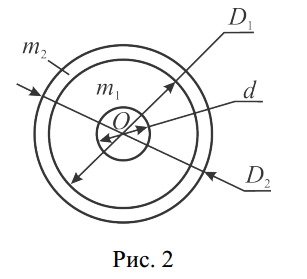
Введем обозначения (см. рис. 2):
m1 – масса стержня с насаженным на него диском;
m2 – масса сменного кольца; d – диаметр стержня;
D1, D2 – внутренний и внешний диаметры сменных колец;
J1 – момент инерции стержня с диском относительно оси О, проходящей через центр инерции маятника перпендикулярно к плоскости диска;
J – момент инерции сменного кольца относительно той же оси;
mS = m1 + m2 — суммарная масса маятника со сменным кольцом;
JΣ = J + J1 — суммарный момент инерции маятника со сменным кольцом относительно оси О.
Наматывая нити подвеса на стержень, можно поднять маятник в верхнее положение А
(см. рис. 1)
За начало отсчета возьмем нижнее положение В, отстоящее от А на расстоянии h.
Когда маятник находится в верхнем положении, он обладает потенциальной энергией
$$U=m_{\sum}gh$$
Формула 1
При раскручивании и опускании маятника происходит переход потенциальной энергии в кинетическую.
Энергия маятника в нижнем положении В определяется только кинетической энергией, которую можно записать в виде
$$K=\frac{m_{\sum}V^2}{2}+\frac{J_{\sum} \omega^2}{2}$$
Формула 2
где v – скорость поступательного движения центра инерции маятника при пересечении им линии В; w – угловая скорость вращения маятника.
В соответствии с законом сохранения энергии
$$m_{\sum}gh=\frac{m_{\sum}V^2}{2}+\frac{ \omega^2 J_{\sum}}{2}$$
Формула 3
Воспользовавшись соотношением V= wd/2 , получим:
$$\frac{m_{\sum}gh}{V^2}=\frac{m_{\sum}}{2}+\frac{2J_{\sum}}{d^2}$$
Формула 4
Если маятник опустился на расстояние h за время t, то из кинематических соотношений для равноускоренного движения следует, что
$$V^2=\frac{4h^2}{t^2}$$
Формула 5
Подставляя (5) в (4), находим
$$J_{\sum}=\frac{m_{\sum}d^2}{4}(\frac{gt^2}{2h}-1)$$
Формула 6
Поскольку моменты инерции системы тел подчиняются правилу аддитивности, т. е. J∑ = J1 + J , то окончательно
$$J=\frac{m_{\sum}d^2}{4}(\frac{gt^2}{2h}-1)-J_1$$
Формула 7
Формулу (7) можно получить также, используя закон движения центра масс и основной закон динамики вращательного движения:
$$\begin{cases}m_{\sum}a=m_{\sum}g-2T\\2T \frac{d}{2}=J_{\sum} \epsilon \end{cases}$$
Формула 8
где Т – сила натяжения подвеса; e – угловое ускорение маятника; а – ускорение центра масс маятника a=ed/2
Решая систему (8) относительно JS, получаем:
$$J_{\sum}=\frac{m_{\sum}d^2}{4}(\frac{g}{a}-1)$$
Формула 9
При подготовке к лабораторной работе убедитесь в этом самостоя- тельно.
Выразив ускорение а через пройденное расстояние h и время t:
$$a=\frac{2h}{t^2}$$
подставив его в (9) и воспользовавшись принципом аддитивности моментов инерции, получим выражение для J, совпадающее с (7).
Таким образом, измеряя время t прохождения маятником расстояния h и зная момент инерции маятника J1, можно найти момент инерции J сменного кольца.
Подготовка установки к работе
- Убедитесь в вертикальном положении стойки 10 и при необходимости произведите регулировку положения основания с помощью регулировочных опор.
- Проследите, чтобы стержень 2 находился в горизонтальном положении. Добиться этого можно с помощью устройства регулировки бифилярного подвеса 7.
- Установите кронштейн с фотодатчиком в нижней части шкалы миллиметровой линейки таким образом, чтобы диск с закрепленным на нем кольцом при движении проходил посередине рабочего окна фотодатчика и не ударялся о кронштейн в нижнем положении.
- Нажмите кнопку «СЕТЬ», расположенную на задней панели электронного блока. При этом должен загореться цифровой индикатор миллисекундомера. Прогрейте установку 3 – 5 минут.
- Нажмите на кнопку «СБРОС».
- Вращая маятник, наматывайте обе нити на стержень виток к витку. Подняв маятник в верхнее положение, зафиксируйте его с помо- щью электромагнитов.
Примечание: В зафиксированном положении нити должны быть слегка ослаблены.
7. Нажмите кнопку «ПУСК», при этом электромагниты обесточиваются, маятник начинает раскручиваться, миллисекундомер начинает отсчет времени, а в момент пересечения маятником оптической оси фотодатчика счет времени прекращается (маятник Максвелла при этом продолжает совершать колебания).
Порядок выполнения работы
- Закрепите на диске маятника одно из сменных колец и зафикси- руйте маятник в верхнем положении. Занесите в табл. 1 величину h хода маятника и массу m2 сменного кольца.
Примечание. Величина h определяется как расстояние от нижнего края сменного кольца, находящегося в верхнем положении, до указателя (метка красного цвета) на нижнем кронштейне.
Таблица 1
h =
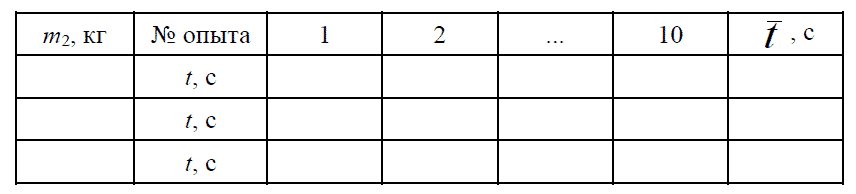
2. Проведите 10 измерений интервала времени t. Результаты зане- сите в табл. 1.
3. Повторите пп. 1 – 2 для каждого из сменных колец.
4. Для каждой из проведенных серий измерений времени t вычислите среднее значение t .
5. Вычислите моменты инерции J сменных колец по формуле (7) и оцените абсолютные погрешности найденных значений (см. приложение). Значения m1 и J1 приведены на установке.
Представьте результаты в виде
$$J_{эксп}=J_{эксп} \pm\triangle J_{эксп}$$
6. Рассчитайте теоретические моменты инерции сменных колец относительно оси вращения, предварительно измерив с помощью штангенциркуля их внутренний D1 и внешний D2 диаметры, по формуле:
$$J_{теор} \approx\frac{m_2}{8}(D_1^2+D_2^2)$$
Формула 10
7. Вычислите для каждого кольца систематическую погрешность моментов инерции (см. приложение). Представьте результаты в виде
$$J_{теор}=J_{теор}\pm \triangle J_{теор}$$
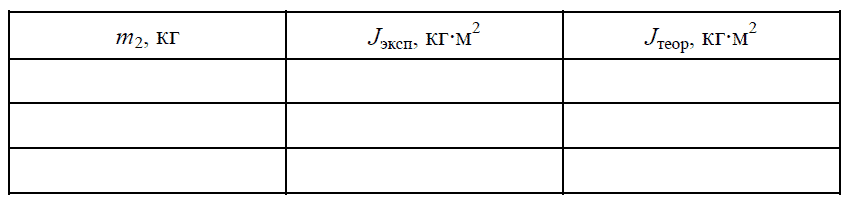
8. Заполните итоговую таблицу результатов (табл. 2).
Таблица 2
D1=
D2=
Вопросы и задания для самоконтроля
-
Сформулируйте закон сохранения механической энергии.
.
-
Что такое момент инерции материальной точки, тела?
.
-
Что представляет собой маятник Максвелла?
.
-
Что такое угловая и линейная скорости, угловое и линейное ускорения? Какова их взаимосвязь?
.
-
Получите соотношение для кинетической энергии вращающегося тела.
.
-
Сформулируйте основной закон динамики вращательного движения.
.
-
Рассчитайте моменты инерции диска, кольца, тонкого кольца
.
(обруча) относительно оси вращения, проходящей через центр масс.
Библиографический список
- Савельев И.В. Курс физики: учебник. Том 1: Механика. Молекулярная физика. М.: Лань, 2008, 4-е изд., стереотип. 354 с.
- Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие для вузов. М.: Академия, 2009, 8-е изд., стереотип. 720 с.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. М.: Академия, 2010, 18-е изд., стереотип. 560 с.
Приложение
- Погрешность при экспериментальном определении момента инерции кольца рассчитывается по формуле
$$\triangle J=\sqrt{(\triangle J_{\sum})^2+(\triangle J_1)^2}$$
Значение ΔJ1 приведено на установке, а значение ΔJΣ вычисляется по формуле
$$\triangle J_{\sum}=J_{\sum}\sqrt{(\frac{\triangle m_{\sum}}{m_{\sum}})^2+(\frac{2 \triangle d}{d})^2+(\frac{2 \triangle t}{t})^2+(\frac{\triangle h}{h})^2}$$
Здесь Δh = 2 мм; ΔmS =1 г; Δd = C/2 , где C – цена деления прибора, которым проводились измерения диаметра стержня. Например, цена деления штангенциркуля составляет 0,1 мм либо 0,05 мм.
Погрешность Δt при определении t состоит из систематической Dtсист и случайной Dtсл составляющих:
$$\triangle t = \sqrt{(\triangle t_{сл})^2+(\triangle t_{сист})^2}$$
Систематическая составляющая погрешности Δtсист =5 мс, а случайная составляющая рассчитывается по формуле
$$\triangle t_{сл}=1,96 \sqrt{\frac{\sum_{i=1}^N (t_i-\overline{t})^2}{N(N-1)}}$$
где n – число измерений времени t.
2. Систематическая погрешность при расчете момента инерции сменного кольца по формуле (10) вычисляется так:
$$\triangle J =J \sqrt{(\frac{\triangle m_{\sum}}{m_{\sum}})^2+(\frac{ \triangle x}{x})^2}$$
где ΔmS =1 г, ΔD (C – цена деления измерительного прибора).
Определение моментов инерции тел с помощью маятника Максвелла: методические указания к лабораторной работе / Рязанский государственный радиотехнический университет; cост.: М.А. Буробин; под ред. О.В. Рожкова. Рязань, 2013. 8 с.
Содержат основные теоретические сведения, порядок выполнения работы и итоговые контрольные вопросы.
Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».
Табл. 2. Ил. 2. Библиогр.: 3 назв.
Маятник Максвелла, вращательное движение, момент инерции, закон сохранения энергии
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ
(зав. кафедрой доц. М.В. Дубков)
Определение моментов инерции тел с помощью маятника Максвелла Составитель: Б уробин Михаил Анатольевич
Редактор Р.К. Мангутова Корректор С.В. Макушина
Подписано в печать 28.01.13. Формат бумаги 60 × 84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТУ.
