Лабораторная работа 1-20: Определение моментов инерции тел методом крутильных колебаний
Цель работы: изучение динамики вращательного движения твердых тел, знакомство с одним из методов определения моментов инерции тел – методом крутильных колебаний.
Приборы и принадлежности: унифилярный подвес ФПМ05, снабженный набором твердых тел (грузов) различной формы и электронным миллисекундомером.
Элементы теории
Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси имеет вид:
$$I \phi^{»}=M$$
Формула 1
М – момент действующих на тело сил, взятый относительно оси вращения;
I – момент инерции тела относительно той же оси;
ϕ′′ – угловое ускорение тела.
Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы m точки и квадрата её расстояния r от оси:
$$I=mr^2$$
Формула 2
Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных материальных точек (элементарных масс △mi ), на которые можно разбить тело:
$$I= \sum_i \triangle m_i r_i^2$$
Формула 3
В предельном случае, когда число элементарных масс стремится к бесконечности, сумма переходит в интеграл:
$$I=\int_m r^2dm= \int_V \rho r^2dV$$
Формула 4
ρ – плотность вещества,
V – объём тела.
Как видно из определения, момент инерции тела есть величина аддитивная: момент инерции тела равен сумме моментов инерции его частей, а момент инерции системы равен сумме моментов инерции тел, входящих в систему.
Существуют различные способы экспериментального определения моментов инерции твердых тел. В данной работе используется метод вращательных (крутильных) колебаний.
Исследуемая система представляет собой твердое тело (например, брусок), подвешенное на струне, концы которой закреплены (рис. 1). После отклонения бруска на некоторый угол j от положения равновесия система начнет совершать крутильные колебания.
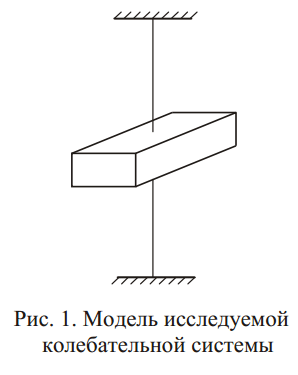
На основании формулы (1) уравнение движения бруска при малых углах отклонения ϕ примет вид:
$$I \phi^{»}=-r \phi^{‘}-k \phi$$
Формула 5
I – момент инерции бруска относительно оси вращения;
r – коэффициент момента сил сопротивления;
k – коэффициент возвращающего (упругого) момента.
Коэффициент r численно равен моменту сил сопротивления при угловой скорости ϕ , равной 1 рад/с. А коэффициент k численно равен моменту упругих сил, возникающих при закручивании нити (струны) на угол, равный 1 рад.
Если сопротивление среды невелико, то первым членом правой части в уравнении (5) можно пренебречь и записать его в виде:
$$I \phi^{»}=-k \phi$$
или
$$\phi^{»}+\frac {k}{I} \phi=0$$
Обозначив kI = w2 , окончательно получим дифференциальное уравнение гармонических колебаний:
$$\phi^{»}+w^2 \phi=0$$
Формула 6
Решение этого уравнения имеет вид:
$$\phi{}(t)= \phi_0 sin(wt+\alpha)$$
Формула 7
ϕ0 – угловая амплитуда колебаний;
w – циклическая частота;
α – начальная фаза.
Как следует из приведенного решения (7), тело будет совершать гармонические колебания около положения равновесия. Циклическая частота w и период колебаний Т определяются величинами I и k по формулам:
$$w=\sqrt{\frac{k}{I}}$$
$$T=\frac{2 \pi}{w}=2 \pi \sqrt{\frac{I}{k}}$$
Формула 8
Описание экспериментальной установки
Работа выполняется на установке – унифилярном подвесе ФПМ05, общий вид которого изображен на рис. 2.
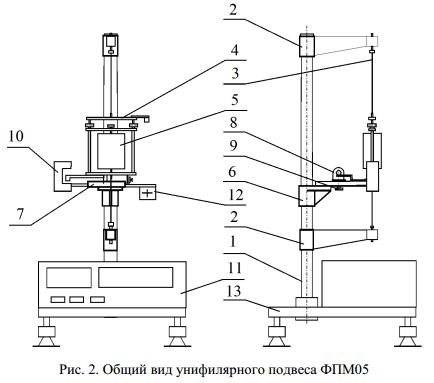
Подвес представляет собой настольный прибор, на вертикальной стойке 1 которого размещены верхний и нижний кронштейны 2. Между кронштейнами 2 на стальной проволоке 3 подвешена рамка 4, предназначенная для установки и закрепления исследуемых тел 5, имеющих различные формы. В центрах граней грузов, в серединах их ребер и у вершин имеются углубления для закрепления в рамке.
На кронштейне 6 размещены: шкала 7, предназначенная для определения начального угла поворота рамки, электромагнит 8 для фиксации рамки в заданном положении и блок питания электромагнита 12. Электромагнит фиксируется в требуемом положении винтом 9.
На том же кронштейне 6 закреплен фотоэлектрический датчик 10. На основании 13 размещен миллисекундомер физический комбинированный 11, служащий для отсчета времени и числа колебаний.
В качестве исследуемых тел используются металлические грузы: цилиндр, параллелепипед и куб. Исследуемый груз закрепляется в рамке, начальное положение которой фиксируется электромагнитом. После отключения электромагнита (тумблер на блоке питания) рамка с грузом начинает совершать крутильные колебания.
Во время колебаний флажок, установленный на рамке, пересекает световой поток в щели фотоэлектрического датчика и сигнал, снимаемый с фотодиода, поступает на миллисекундомер.
Метод крутильных колебаний
Этот метод заключается в следующем. Тело с неизвестным моментом инерции I закрепляют в рамке подвеса. Период колебания такой системы будет равен
$$T=2 \pi \sqrt{\frac{I_0+I}{k}}$$
Формула 9
I0 – момент инерции ненагруженной рамки,
k – коэффициент упругости проволоки подвеса.
Согласно формуле (9) момент инерции I исследуемого тела можно вычислить, зная величины T, I0 и k. Период T колебаний несложно определить, измерив время t, за которое совершается N полных колебаний:
$$t=NT=2 \pi N \sqrt{\frac{I_0+I}{k}}$$
Формула 10
Для того, чтобы исключить неизвестные величины I0 и k, нужно измерить время t0 колебаний ненагруженной рамки, а также время tЭ колебаний рамки, нагруженной эталонным телом – телом с известным моментом инерции IЭ.
Таким образом, получаем систему уравнений:
$$\begin{cases}t^2= 4 \pi ^2 N^2 (I_0+I)/k \\t_0^2= 4 \pi ^2 N^2 I_0/k \\ t_Э^2= 4 \pi ^2 N^2 (I_0+I_Э)/k\end{cases}$$
Формула 11
Решая данную систему уравнений, получаем формулу для момента инерции выбранного нами тела:
$$I=I_Э \frac{t^2-t^2_0}{t_Э^2-t^2_0}$$
Формула 12
Из выражения (12) следуют формулы для предельной относительной погрешности определяемого момента инерции:
$$\begin{cases} E_I=E_{Iэ}+\frac{2 \triangle t (t+t_э)}{(t+t_0))(t_э-t_0)}, при & t>t_э; \\ E_I=E_{Iэ}+\frac{2 \triangle t (t+t_э)}{(t-t_0))(t_э+t_0)}, при & t_э>t; \\ \end{cases}$$
Формула 13
EIэ = △Iэ / Iэ – относительная погрешность момента инерции эталонного тела;
△ t – погрешность измерения промежутка времени N полных колебаний рамки (предполагается, что эта погрешность одинакова для всех трех случаев измерения: t0, t и tэ).
Формулы (12) и (13) являются основными формулами для обработки результатов измерений, однако расчет существенно упрощается, если формулу (12) переписать в виде:
$$I=I_э \frac{t-t_0}{t_э-t_)}[1+\frac{t-t_э}{t_э+t_0}]$$
Формула 14
Если, кроме того, измеряемые промежутки времени t и tэ различаются незначительно, то малым по сравнению с единицей членом но пренебречь и представить (14) в виде:
$$I=I_э \frac{t-t_0}{t_э-t_0}$$
Формула 15
Справедливость формулы (15) проверяется путем сравнения величины (t — tэ ) (tэ + t0 ) с относительной погрешностью результата EI , определяемой уравнением (13). Она справедлива, если:
$$E_I=\frac{\triangle I}{I}\geq\frac{|t-t_э|}{t_э+t_0}$$
Формула 16
Из уравнения (13) также следует, что чем больше полное время колебаний рамки, тем точнее получается результат. Поэтому в процессе прямых измерений рекомендуется измерять времена t0, t и tэ для
N = 50 колебаний рамки.
Задание
В задание входит определение моментов инерции двух тел различной формы относительно их центра масс теоретически и экспериментально.
Для теоретического расчёта моментов инерции по известным массам и размерам тел используются следующие выражения:
$$I_ц=\frac{1}{2}m_цR^2$$
$$I_n=\frac{1}{12}m_n (a^2+b^2)$$
Формула 17
Iц и Iп — моменты инерции цилиндра и параллелепипеда соответственно;
mц и mn массы тел;
R – радиус цилиндра;
a, b – размеры параллелепипеда.
Расчёт моментов инерции данных тел по экспериментально полученным данным производится по формулам (14) или (15). Необходимо также оценить абсолютные и относительные погрешности рассчитанных моментов инерции исследуемых грузов.
Порядок выполнения работы
Подготовка установки к работе
- Включите в сеть шнур питания миллисекундомера. Нажмите кнопку «СЕТЬ» на лицевой панели, при этом должны загореться цифровые индикаторы.
- После прогрева миллисекундомера (1–2 минуты) включите тумблер блока питания электромагнита.
- Ослабив стопорный винт электромагнита, установите его на угол, указанный преподавателем, в пределах 60-100º. Зафиксируйте электромагнит в этом положении тем же самым винтом.
- Поверните рамку так, чтобы металлический флажок, установленный на рамке, коснулся якоря электромагнита. При этом флажок притянется к якорю и рамка займет фиксированное положение.
- С помощью кнопок «СТОП» и «СБРОС» миллисекундомера обнулите счетчики числа и времени колебаний. Прибор готов к работе.
Проведение измерений
- Выключите тумблер блока питания электромагнита, при этом рамка начнет совершать колебательное движение и запустятся счетчики миллисекундомера. После N–1 полных колебаний рамки нажмите кнопку «СТОП» – отсчетное устройство, доработав до конца 50-го колебания, остановит счетчики. Запишите время t0 – время 50-ти колебаний ненагруженной рамки. Число полных колебаний рамки может быть задано преподавателем дополнительно в пределах 30-60.
Остановив рукой колеблющуюся рамку, повторите операции, описанные в пп. 1.4, 1.5 и 2.1, еще два раза. Результаты измерений занесите в заранее подготовленную таблицу.
- Для закрепления исследуемого тела в рамке остановите рамку и освободите подвижную планку, отвернув гайки боковых цанг.
- Поднимите планку по направляющим и, придерживая её рукой, установите груз так, чтобы соответствующее углубление в центре одной из граней вошло в выступ на нижней перекладине рамки.
- Опустите подвижную планку по направляющим, затяните гайки боковых цанг и подожмите исследуемое тело винтом, находящимся на подвижной планке.
- Включите электромагнит и повторите операции, описанные в пп. 1.4, 1.5 и 2.1, три раза, результаты измерений занесите в таблицу.
- Для замены груза остановите рамку, отпустите гайки боковых цанг, переместите подвижную планку вверх и замените первый груз на второй, закрепив его в рамке, как указано в п. 2.4.
- Измерьте время 50-ти полных колебаний второго груза и эта- лонного тела по методике, описанной выше. В качестве эталонного тела можно использовать куб или цилиндр по указанию преподавателя. Результаты измерений занесите в таблицу.
- Измерьте размеры исследуемых тел простейшим измерительным прибором (штангенциркулем) и запишите эти значения, а также массу грузов в отчёт о лабораторной работе.
Порядок расчёта
- По выражениям (17), определяющим моменты инерции данных тел через массу и размеры, рассчитайте момент инерции эталонного тела (цилиндра или куба по указанию преподавателя). Оцените абсолютную погрешность по формулам:
$$\triangle J_{эц}=2< J_{эц}> \frac{\triangle R}{R}$$
$$\triangle J_{эк}=2< J_{эк}> \frac{\triangle a}{a}$$
Формула 18,19
R – радиус цилиндра;
a – сторона куба;
Jэц и Jэк моменты инерции цилиндра и куба, рассчитанные по выражениям (17);
△R и △a – систематическая погрешность измерений радиуса цилиндра и стороны куба соответственно.
- Рассчитайте относительную погрешность момента инерции эталонного тела.
- Используя данные таблицы, вычислите абсолютную и относительную погрешности измеренных промежутков времени t0 , t1 , t2 .
- По средним значениям промежутков времени N полных колебаний рамки с исследуемыми телами и без оцените относительные погрешности моментов инерции исследуемых тел по выражению (13).
Сравните последние с величиной |t — tэ| / (tэ + t0 ) . Если неравенство (16) выполняется, то расчёт моментов инерции исследуемых грузов можно производить, применяя упрощённую формулу (15). В противном случае нужно использовать более точное выражение (14). Рассчитайте по соответствующим формулам моменты инерции исследуемых тел, а также абсолютные погрешности этих моментов инерции.
- По выражениям (17) вычислите теоретические моменты инерции исследуемых тел через массу и размеры. Оцените абсолютные по- грешности полученных значений моментов инерции по формулам (18) и (19), а также относительные погрешности.
- Сравните экспериментально полученные значения моментов инерции исследуемых тел с результатами расчётов по теоретическим формулам и сделайте соответствующие выводы.
Вопросы и задания для самоконтроля
-
Сформулируйте основной закон динамики вращательного движения твердого тела.
.
-
Дайте определение момента инерции твердого тела. Как его рассчитать теоретически?
.
-
Получите дифференциальное уравнение крутильных колебаний, прокомментируйте его.
.
-
Запишите уравнение колебательного движения крутильных колебаний. Чем определяется их период?
.
-
Каковы прямые измерения в данной работе? В чем состоит роль эталонного тела?
.
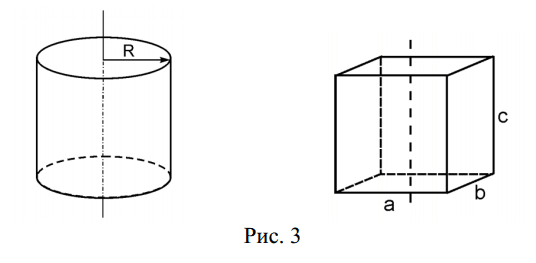
Используя формулу (4), покажите, что моменты инерции цилиндра и прямоугольного параллелепипеда (рис. 3) относительно вертикальной оси их симметрии, проходящей через центр их масс, определяются выражениями (17).
Библиографический список
- Савельев И.В. Курс физики: учебник. 4-е изд. т. 1: Механика. Молекулярная физика. М.: Лань, 2008. 354 с.
- Детлаф А.А., Яворский Б.М. Курс физики: учеб. пособие для вузов. 8-е изд. М.: Академия, 2009. 720 с.
- Трофимова Т.И. Курс физики: учеб. пособие для вузов. 18-е изд. М.: Академия, 2010. 560 с.
УДК 537.226.4
Определение моментов инерции тел методом крутильных колебаний: методические указания к лабораторной работе / Рязанский государственный радиотехнический университет; cост.: М.А. Буробин, А.В. Брыков, Ю.В. Черкасова. Рязань, 2016. 8 с.
Представлена краткая теория крутильных колебаний, описан метод унифилярного подвеса. Приводятся порядок выполнения работы, методические указания по расчету погрешностей, контрольные вопросы и список рекомендуемой литературы.
Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».
Табл. 1. Ил. 3. Библиогр.: 3 назв.
Вращательное движение твердого тела, момент инерции, крутильные колебания
Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)
Определение моментов инерции тел методом крутильных колебаний Составители: Буробин Михаил Анатольевич
Брыков Александр Валериевич Черкасова Юлия Вадимовна
Редактор М.Е. Цветкова Корректор С.В. Макушина
Подписано в печать 15.02.16. Формат бумаги 60×84 1/16.
Бумага писчая. Печать трафаретная. Усл. печ. л. 0,5.
Тираж 200 экз. Заказ
Рязанский государственный радиотехнический университет.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТУ.
