МУ 4820: Изучение измерительных приборов. Оценка погрешностей измерений физических величин

Лабораторная работа 1-1: Изучение измерительных приборов. Оценка погрешностей измерений физических величин

Цель работы: изучить порядок оценки погрешностей при прямых и косвенных измерениях физических величин; ознакомиться с устройством, принципом действия простейших измерительных приборов; определить линейные размеры и объем заданного тела.

Приборы и принадлежности: штангенциркуль, микрометр, исследуемое тело.

ЭЛЕМЕНТЫ ТЕОРИИ

Основные понятия

Измерение физической величины — процесс сравнения измеряемой величины с помощью технических средств с однородной ей величиной, условно принятой за единицу.

Различают прямые и косвенные измерения.

Прямым измерением называют измерение, при котором искомое значение величины находят непосредственно из данных опыта.

Косвенным измерением называют измерение, при котором искомое значение величины находят на основании известной функциональной зависимости между ней и величинами, являющимися результатами прямых измерений.

Погрешность измерения есть величина отклонения результата измерений от истинного (действительного) значения измеряемой величины.

Действительное значение физической величины есть ее значение, найденное экспериментальным путем и максимально приближенное к истинному значению. В качестве действительного значения может быть использовано среднее арифметическое отдельных измерений:

где x_i — результат i-го замера величины x, n — число измерений

Абсолютная    погрешность    —    погрешность,    выраженная    в единицах измеряемой величины:

Относительная погрешность — погрешность, выраженная отношением абсолютной погрешности к действительному значению измеряемой величины:

$$\delta_i=\frac{\triangle x_{i}}{ < x> }$$

Погрешность, представленная в любом виде, может содержать систематическую и случайную составляющие.

Систематическая — погрешность, сохраняющая постоянное значение и знак или меняющаяся по известному закону при повторных измерениях одной и той же величины в одинаковых условиях.

Случайная — погрешность, возникающая при повторных измерениях одной и той же величины в одинаковых условиях и имеющая случайные (непредсказуемые) значения.

Грубые погрешности («промахи») — отклонения, которые существенно отличаются от ожидаемых при данных условиях значений погрешности.

Доверительная вероятность — отношение числа результатов измерений в некотором диапазоне значений измеряемой величины к общему (достаточно большому) числу полученных результатов, т.е. доля результатов, соответствующих некоторому диапазону значений измеряемой величины,

Доверительный интервал — диапазон значений измеряемой величины, соответствующий некоторому (выбранному) значению доверительной вероятности.

Коэффициент Стьюдента — коэффициент, учитывающий изменение ширины доверительного интервала при использовании конечного числа проведенных замеров измеряемой величины.

Средняя арифметическая погрешность измерения физической величины

где Dx_i — абсолютная погрешность i-го измерения величины x.

Среднеквадратичное отклонение результата измерения величины

Порядок оценки погрешности при прямых измерениях физической величины x

1. Проведение замеров величины x. Результаты измерений, полученные при выполнении опыта, заносятся в таблицу.
2. Исключение «промахов». Введение поправок на известную постоянную систематическую погрешность (например, смещение стрелки измерительного прибора с нулевого положения, влияние изменения температуры при проведении измерений и др.)
3. Заполнение таблицы скорректированных результатов измерений величины x. x₁, x₂, …, x_n — значения измерений, n — число измерений.
4. Расчет действительного (среднего) значения <x> по формуле (1).
5. Расчет абсолютной   погрешности   по   формуле   (2).   Должно выполняться условие

$$\sum_{i=1}^n\triangle x_{i}\approx 0, т.е. сумма \ll \triangle x_{i}$$

6. Оценка     систематической     составляющей     среднеквадратичного отклонения

$$\sigma_c=\frac{\triangle_{c}}{\sqrt{3}} $$

Формула 7

где D_с — систематическая погрешность, определяемая как

$$\triangle_{c}=\begin{cases}k\frac{c}{2} & \\k\gamma\frac{A_{N}}{100} & \end{cases}$$

с — цена деления измерительного прибора, g — класс точности измерительного прибора, A_N — нормативный множитель, определяемый классом точности, k — коэффициент, определяемый выбранной доверительной вероятностью P согласно таблице:

В лабораторном практикуме выбирается Р = 0,95.

7. Оценка случайной составляющей среднеквадратичного отклонения

$$ \sigma_{сл}=\sqrt{\frac{\sum_{i=1}^n (\triangle x_i)^2}{n(n-1)}} $$

Формула 9

8. Расчет суммарной среднеквадратичной погрешности

$$\sigma=\sqrt{\sigma_{c}^2+\sigma_{сл}^2}$$

Формула 10

Замечание: если величина s используется для расчета погрешности косвенного измерения, то дальнейшие расчеты погрешности прямого измерения можно не производить.

• Определение коэффициента Стьюдента t_c. Коэффициент Стьюдента находится из таблицы по известному числу измерений n и доверительной вероятности P:

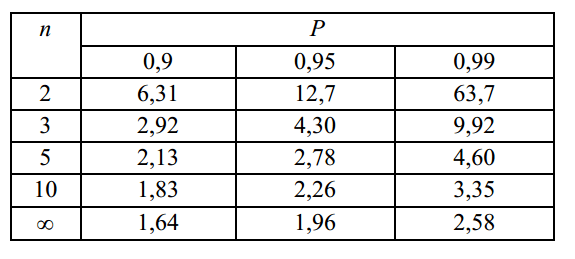
10. Оценка случайной погрешности по формуле

$$\triangle_{сл}=t_c +\sigma_{сл} $$

11. Оценка полной абсолютной погрешности результата измерения величины x:

12. Расчет относительной погрешности величины x:

 $$\delta_{x}=\frac{\triangle x}{< x>} $$

13. Запись результата измерения величины x:

Порядок расчета погрешности при косвенных измерениях физической величины

1. Расчет   среднего   значения   искомой   величины   А.   Для   расчета используется формула из описания метода измерения:

< A >= f (< x >, < y >,…, a,b,…) ,                                                              (14)

где <x>,<y>,… — средние значения аргументов функции

А (x, y, …), полученные при прямых измерениях, a, b — постоянные величины.

2. Расчет величины

где δA/δx, δA/δy — соответствующие частные производные [например, δA/δx — это производная функции A (x, y, …), полученная при дифференцировании по x, остальные переменные y, … считаются постоянными величинами], а σ_x , σy , … — суммарные среднеквадратичные погрешности аргументов функции A (x, y, …), найденные по формуле (10), σ_ca , σ_cb , … — систематические составляющие среднеквадратичного отклонения величин a, b,…, определяемые по формуле (7)

3. Расчет абсолютной погрешности величины А:

где t_c∞ — коэффициент Стьюдента, определяемый для выбранной доверительной вероятности Р и числа измерений n = ∞ . Для лабораторных работ принимают Р = 0,95, t_c ∞ = 1,96.

• Расчет относительной погрешности величины x:

Если функция А имеет вид   A = x^a*y^b*z^g , где x, y, z — величины,

полученные    прямыми    измерениями,    то    d_А   можно    найти    по упрощенной формуле

5. Запись результата измерения величины:

Правила записи и вычислений

Все цифры в записи числа, кроме нулей в левых разрядах, называются значащими. Например, числа 0,035; 3,5; 3,5×10⁶; 0,35 имеют по две значащие цифры. При записи результатов измерений необходимо действовать по следующим правилам.

Величину (цифру) абсолютной погрешности округляют до двух значащих цифр.

Численное значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.

Нуль записывают так же, как и другие цифры в последнем разряде. Он показывает точность округления.

Все    результаты    измерений,    в   том   числе    и    повторяющиеся, заносятся в таблицу.

При вычислениях все числа округляют так, чтобы младший разряд любого числа был тем же, что и последний разряд числа с наибольшей абсолютной погрешностью.

Округляют погрешности предварительно в сторону завышения.

Примечание.   

Вычисления,    произведенные     с    большим    числом десятичных знаков, чем это необходимо, создают ложное впечатление о     большей   точности   измерений.    Точность   обработки   числового материала должна быть согласована с точностью измерений. Для этого следует придерживаться правила: ошибка, получающаяся в процессе вычислений, должна быть примерно на порядок меньше суммарной погрешности измерений. Кроме того, при вычислениях случайных     погрешностей             среднюю       квадратичную погрешность определяют с одной значащей цифрой, если она больше 3, и с двумя значащими цифрами, если первая из них меньше 4. Например, 2,357 округляют до 2,36, а 2,415 – до 2,4.

Оформление отчета

Отчет о лабораторной работе готовится на двойных тетрадных листах. На первой странице оформляется титульный лист:

Основные требования к оформлению отчета:

1. Все записи должны быть настолько полными, чтобы были понятны любому достаточно квалифицированному читателю, а не только автору.
2. Записи должны быть по возможности краткими, чертежи и графики выполнены на бумаге с сеткой.
3. Чертежи, графики, таблицы снабжаются заголовками или подписями с расшифровкой обозначений.
4. Отчет должен отображать всю проделанную работу. Общий объем отчета не должен превышать 8 с.

ИЗУЧЕНИЕ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Нониусом называется вспомогательная шкала, с помощью которой производят отсчет долей делений основной шкалы измерительных приборов. Существуют нониусы линейные, спиральные, угломерные (угловые) и другие. Принцип получения всех нониусов одинаков. Рассмотрим линейный нониус. Это дополнительная линейка, скользящая вдоль основной шкалы. Пусть число делений нониусной шкалы будет n, длина одного ее деления y, длина наименьшего деления основной шкалы x. Если будет выполняться соотношение ny=(n±1)x, то эти две линейки образуют нониус. В случае выполнения условия ny=(n-1)x имеем нониус первого рода или прямой. Разность (20) называется точностью нониуса.

Рассмотрим процесс измерения с помощью линейного нониуса (рис. 1). Пусть l — измеряемый отрезок. Совместим его начало с нулевым делением основной шкалы, и пусть при этом его конец окажется между m-м и (m+1) -м делениями этой шкалы. Тогда l = mx+D, где D — неизвестная пока доля (m+1)-го деления основной шкалы, определяемая с помощью нониуса. Совместим с концом отрезка l нуль нониуса. Так как деления нониуса не равны делениям основной шкалы, то обязательно на нем найдется такое деление k, которое совпадает с каким-то (m+i)-м делением основной шкалы. Из рис. 1 видно, что расстояние AB между m-м и (m+i)-м делениями основной шкалы выражается через деления нониуса, то есть

Подставив сюда y из равенства (20), получим

где k — целое число. Так как k<n, kx/n < n. Величина Δ также меньше x, но поскольку AB содержит число делений x (рис 1), то разность

$$(\triangle — \frac {k}{n}x) $$

в формуле 22 должна быть равна 0. Отсюда

$$\triangle =\frac {k}{n}x$$

Таким образом, длина отрезка

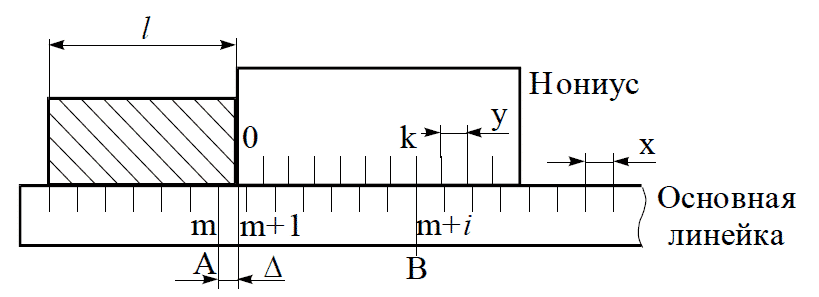
Это значит, что длина отрезка, измеряемого с помощью нониуса, равна числу целых делений основной шкалы плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением основной шкалы. Погрешность нониуса равна половине его точности.

Штангенциркуль служит для линейных измерений, не требующих высокой точности. Отсчетными приспособлениями у всех конструкций штангенинструментов служат шкала штанги и линейный нониус. Цена деления основной шкалы штанги обычно равна одному миллиметру, а нониусы обычно имеют точность отсчета 0,1; 0,05; 0,02 мм.

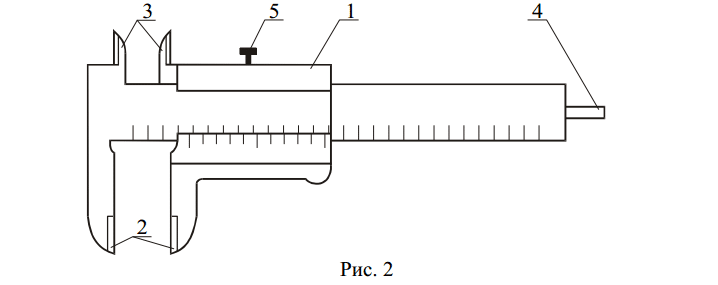
Нониус укреплен в подвижной рамке (или нанесен на нее), скользящей вдоль основной шкалы штанги. При нулевом показании инструмента нуль нониуса совпадает с нулевым штрихом основной шкалы. При измерении детали подвижная рамка 1 с нониусом смещается и деталь зажимается губками 2 штангенциркуля (рис. 2). Существует несколько видов штангенциркулей. Они различаются типом и количеством измерительных губок, длиной штанги, типом нониусов или наличием вспомогательных деталей. При наличии у штангенциркуля верхних 3 и нижних 2 измерительных губок его можно применить для измерения как внутренних, так и внешних размеров. Часто штангенциркуль снабжается линейкой 4, служащей для измерения глубин. Винт 5 служит для закрепления рамки при измерениях.

Для более точных измерений применяют микрометрические инструменты. Они бывают нескольких типов: микрометр для наружных измерений, микрометрический глубиномер и микрометрический нутромер. Микрометр для наружных измерений обычно представляет собой металлическую скобу 5 с цилиндром 6, на концах которой находятся неподвижный упор 2 и полый стержень 3, в который ввинчен микрометрический винт (рис. 3).

При измерении предмет зажимается между упором 2 и подвижным концом стержня 3. Микровинт вращают трещоткой 4, при этом корпус барабана 1 перемещается поступательно относительно цилиндра 6.

Отсчет ведется по горизонтальной шкале, нанесенной на цилиндр 6, и по шкале барабана. Горизонтальная шкала представляет собой двойную шкалу с ценой деления 0,5 мм, нанесенную на обе стороны продольной черты таким образом, что верхняя шкала сдвинута относительно нижней на половину деления. Цена деления шкалы барабана может быть установлена следующим образом: пусть число делений круговой шкалы барабана n=50, а шаг микровинта h=0,5 мм. В этом случае одному полному обороту микровинта (а следовательно, и барабана) соответствует линейное перемещение края барабана и стержня 3 на 0,5 мм, т.е. линейному перемещению 1 мм соответствуют 2 оборота барабана. Значит, цена деления круговой шкалы

a = h/n = 0,01мм.

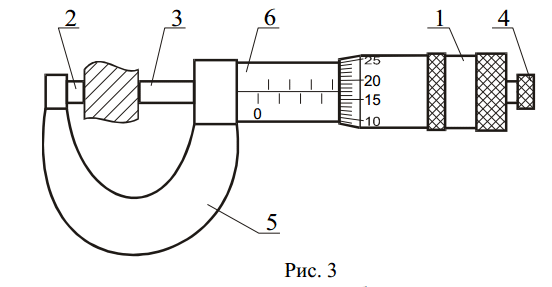
Отсчет производится следующим образом: по шкале стержня отсчитывается размер измеряемого предмета с точностью до 0,5 мм. Сотые доли миллиметра отсчитываются по круговой шкале барабана. Полученные результаты складываются. Порядок отсчета одинаков для всех микрометрических инструментов. На рис. 3 изображено для примера положение барабана, соответствующее длине 3,67 мм. На скобе микрометра обычно указываются пределы измерения: 0-25 мм, 0-50 мм и т.д.

Прежде чем приступить к измерениям с помощью микрометра, нужно убедиться в том, что при доведении винта до упора с помощью трещотки получается по обеим шкалам нулевой отсчет.

Необходимо иметь в виду, что правильный результат можно получить лишь в том случае, если измеряемый предмет зажимается с помощью трещотки.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Ознакомьтесь с измерительными инструментами. Определите цену деления шкалы и нониуса.
2. Измерьте высоту и диаметр исследуемого тела (сделать по 5 замеров каждого размера штангенциркулем, затем микрометром). Данные занесите в таблицы отдельно для измерений штангенциркулем и микрометром.
3. Рассчитайте погрешности прямых измерений высоты и диаметра при использовании штангенциркуля и микрометра, занося промежуточные    результаты    в   таблицу.    Запишите    результаты прямых измерений h и d.
4. Рассчитайте объем исследуемого тела по результатам измерений штангенциркулем и микрометром. Сравните полученные данные.
5. Рассчитайте    погрешности    для   полученных   значений    объемов исследуемого тела.
6. Запишите   окончательные   результаты   для   измерений   объема   с помощью штангенциркуля и микрометра в таблицу.

Таблица экспериментальных данных

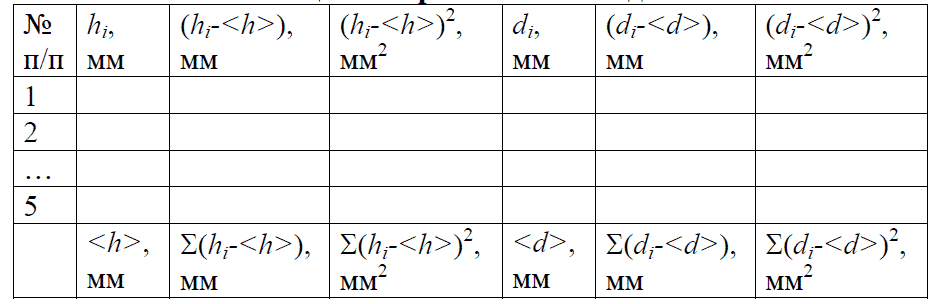
Вопросы для самоконтроля и ответы на них

Библиографический список

1. Физический практикум. Механика и молекулярная физика /Под ред. В.И.Ивероновой. М.: Наука, 1967. С. 40-48.
2. Лабораторные занятия по физике / под ред. Л.Л.Гольдина. М.: Наука, 1983. С. 11-39.
3. Введение в физический лабораторный практикум: методические указания / Рязан. радиотехн. ин-т; сост.: А.Ю. Борисова, Н.В. Веселкин и др. Рязань, 1988. 40 с.

УДК 620.099.32

Изучение измерительных приборов. Оценка погрешностей измерений физических величин: методические указания к лабораторной работе / Рязан. гос. радиотехн. ун-т; сост.: Т.Г. Авачёва, М.В. Дубков, А.В. Николаев; Рязань, 2014. 12 с.

Изложены основные понятия и порядок оценки погрешностей результатов измерений при выполнении лабораторных работ по курсу общей физики. Содержат сведения о простейших измерительных приборах.

Предназначены для студентов всех специальностей дневной и вечерней форм обучения.

Табл. 1. Ил. 3. Библиогр.: 3 назв.

Измерение, погрешность, штангенциркуль, микрометр, нониус

Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.

Рецензент: кафедра общей и экспериментальной физики РГРТУ (зам. зав. кафедрой доц. М.А. Буробин)

Изучение измерительных приборов.

Оценка погрешностей измерений физических величин

Составители: Авачёва Татьяна Геннадиевна

Дубков Михаил Викторович

Николаев Артём Владимирович

Редактор Р.К. Мангутова Корректор С.В. Макушина

Подписано в печать 30.06.14. Формат бумаги 60 ´ 84 1/16. Бумага газетная. Печать трафаретная. Усл. печ. л. 0,75.

Тираж 200 экз. Заказ            .

Рязанский государственный радиотехнический университет.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТУ.